Inverse Projection

一种从NDC坐标到ViewPos的代码可以写做(见：https://stackoverflow.com/questions/11277501/how-to-recover-view-space-position-given-view-space-depth-value-and-ndc-xy)

mat4 inversePrjMat = inverse( prjMat );
vec4 viewPosH      = inversePrjMat * vec3( ndc_x, ndc_y, 2.0 * zdepth - 1.0, 1.0 )
vec3 viewPos       = viewPos.xyz / viewPos.w;

自己尝试着用Sympy推了一下能推出近似的结果，但是不能完全消元，不知道是哪弄错了还是怎么，推导过程见附录。这篇文章介绍了这一段代码的干净代数推导方式。

已知

\[v_{ndc} = v_{clip} / v_{clip}.w\]

\[\mathbf{P} v_{view} = v_{clip}\]

带入，左右两边乘以inv(P)

\[v_{view} = \mathbf{P}^{-1}v_{ndc} * v_{clip}.w \]

\(v_{clip}.w\)是未知标量，然而，已知\(v_{view}.w\)等于1,可知

\[ 1 = (\mathbf{P}^{-1}v_{ndc}).w * v_{clip}.w \]

\[ v_{clip}.w = \frac{1}{(\mathbf{P}^{-1}v_{ndc}).w } \]

因此

\[v_{view} = \frac{\mathbf{P}^{-1}v_{ndc}} {(\mathbf{P}^{-1}v_{ndc}).w }\]

从ViewSpace到WorldSpace是trivial的就不推了。

Interpolated Ray

这种方法不展开说，Unity Shader入门精要里给了详细推导。简单地说就是

在CPU端记录相机的WorldPos
在VertexShader里记录世界坐标系下相机到近裁剪平面的四个角的Vector

\[ \begin{aligned} halfHeight &= NearPlane * tan(\frac{fov}{2})\\ toTop &= camera.up \times halfHeight\\ toRight &= camera.right \times halfHeight \times aspectRatio\\ TopLeft &= camera.forward * Near + toTop - toRight\\ \end{aligned} \]

在vertex到fs过程中GPU会插值每个像素(后处理是渲染一个Quad或者一个三角形)

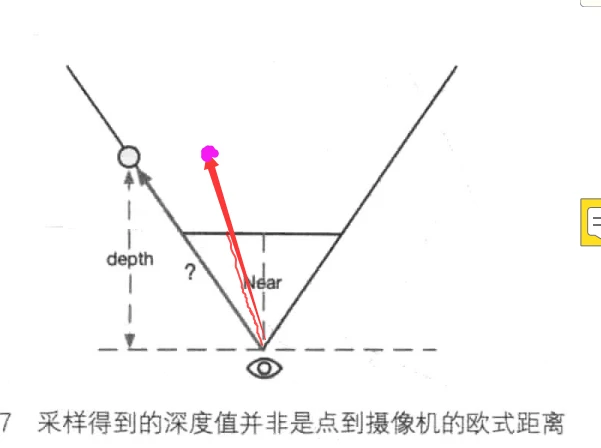
从NDC到View_World_Space坐标推导-2022-08-15-00-43-07

可以得到某个点的坐标等于

\[ worldPos = InterpolatedRay * depth / Near \]

Reference

已知OpenGL的投影矩阵\(\mathbf{P}\)

\[ \mathbf{P} = \left[\begin{array}{cccc} \frac{2 n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2 n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2 f n}{f-n} \\ 0 & 0 & -1 & 0 \end{array}\right] \]

在\( r = -l \),\(t = -b\)的时候可以简化(这个是常见情况)

使用Sympy推导

T11,T22,T33,T34,T43 = symbols('T11 T22 T33 T34 T43',real=True)
P_m = Matrix([[T11,0,0,0],[0,T22,0,0],[0,0,T33,T34],[0,0,T43,0]])
xv,yv,zv = symbols('x_v y_v z_v',real=True)
V_view = Matrix([xv,yv,zv,1])
V_clip = P_m * V_view
V_ndc = V_clip / V_clip[3]
P_m_inv = P_m.inv()
V_ndc_inv = P_m_inv * V_ndc
eq1 = V_ndc_inv / V_ndc_inv[3]
eq2 = eq1.subs(T43,-1)
f,n = symbols("f n",real=True)
eq3 = eq2.subs(T33,-(f + n) / (f - n))
eq4 = eq3.subs(T34,-2*f*n / (f - n))
display(eq4)
eq5 = eq4.subs({f:1000.0,n:0.01})
display(eq5)

其中eq4的输出为

\[ \left[\begin{matrix}- \frac{x_{v}}{z_{v} \left(- \frac{- f - n}{2 f n} + \frac{\left(f - n\right) \left(- \frac{2 f n}{f - n} + \frac{z_{v} \left(- f - n\right)}{f - n}\right)}{2 f n z_{v}}\right)}\\- \frac{y_{v}}{z_{v} \left(- \frac{- f - n}{2 f n} + \frac{\left(f - n\right) \left(- \frac{2 f n}{f - n} + \frac{z_{v} \left(- f - n\right)}{f - n}\right)}{2 f n z_{v}}\right)}\\- \frac{1}{- \frac{- f - n}{2 f n} + \frac{\left(f - n\right) \left(- \frac{2 f n}{f - n} + \frac{z_{v} \left(- f - n\right)}{f - n}\right)}{2 f n z_{v}}}\\1\end{matrix}\right] \]

随便代入个f,n,代入f=1000,n=0.01后

\[ \left[\begin{matrix}- \frac{x_{v}}{z_{v} \left(50.0005 + \frac{49.9995 \left(- 1.0000200002 z_{v} - 0.020000200002\right)}{z_{v}}\right)}\\- \frac{y_{v}}{z_{v} \left(50.0005 + \frac{49.9995 \left(- 1.0000200002 z_{v} - 0.020000200002\right)}{z_{v}}\right)}\\- \frac{1}{50.0005 + \frac{49.9995 \left(- 1.0000200002 z_{v} - 0.020000200002\right)}{z_{v}}}\\1\end{matrix}\right] \]

把第三项单独拿出来,这个式子应该等于\(z_v\)

\[ -\frac{1}{50.0005 + \frac{49.9995 \left(- 1.0000200002 z_{v} - 0.020000200002\right)}{z_{v}}} \]

该式粗略化简约等于 \(\frac{z_v}{0.02 * 49.9995}\)，约等于\(z_v\)。

从NDC到View Space坐标推导

Inverse Projection

Interpolated Ray

Reference