One approach to implementing a plane mirror is to render objects twice: once in their original positions, and again as a mirror reflection.

Reflected matrix with a given plane

DirectX offers a convenient function XMMatrixReflect for reflecting objects. The function takes normalized Point-Normal form of plane as an argument, which is \( ax + by + cz + d = 0, \vec{n} = \{a,b,c\}\). It then returns a matrix can be used to mirror object vertices.

The Pseudocode is

auto plane = vec4(0,0,1,0); // x-y plane
auto reflectMatrix = XMMatrixReflect(plane);

auto World = translate(...);
DrawObject(World,View,Proj);

auto Reflected = World * reflectMatrix;
DrawObject(Reflected,View,Proj);

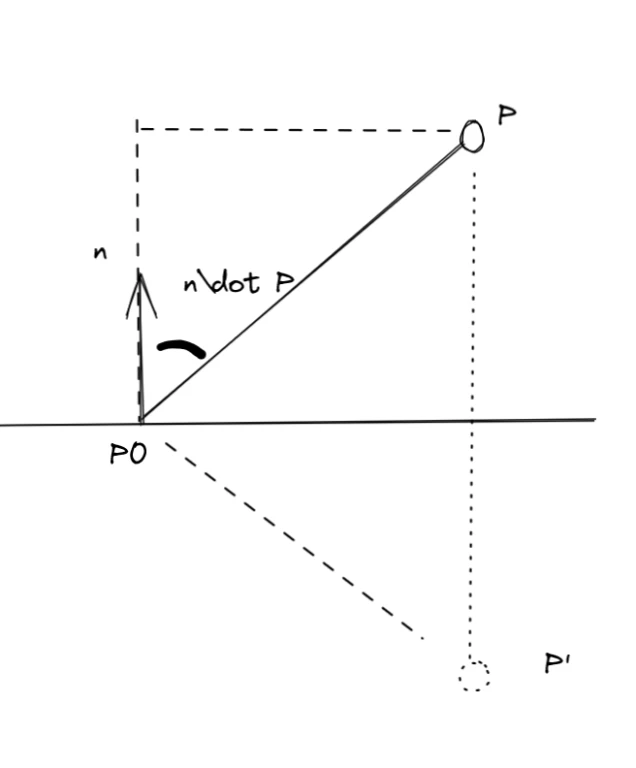
Rendering_Objects_Mirror_Reflected-2023-03-11-01-03-22

\[ P' = P - 2(\vec{n} \cdot \vec{P_0P})\vec{n} \]

In this equation, \(2(\vec{n} \cdot \vec{P_0P})\) is a scalar.

It's worth noting that the normalized point-normal plane can also be expressed as follows:

for any point \(\vec{x}\) on the plane

\[ \vec{n} \cdot x + d = 0 \]

Expanding \(\vec{P_0P}\) to \((P - P_0)\), we can write:

\[ P' = P - 2(\vec{n} \cdot P - \vec{n} \cdot P_0)\vec{n} \]

then

\[ P' = P - 2(\vec{n} \cdot P + d)\vec{n} \]

we expand the vector form to homogeneour coordinates. \(\bf{P}\) is a point with fourth component of 1, while \(\vec{n}\) is normal vector with a fourth component of 0.

\[ P' = \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} - \begin{bmatrix} 2n_x(n_xP_x + n_yP_y + n_zP_z + d) \\ 2n_y(n_xP_x + n_yP_y + n_zP_z + d) \\ 2n_z(n_xP_x + n_yP_y + n_zP_z + d) \\ 0 \end{bmatrix} \]

After simplifying the equation, we can express it as the dot product of a matrix and the point \(P\). Assuming that the dot product is performed by left-multiplying the matrix and the point (as per the convention in OpenGL), we can write:

\[ \begin{bmatrix} 1 - 2n_xn_x & -2n_xn_y & -2n_xn_z & -2n_xd \\ -2n_yn_x & 1-2n_yn_y & -2n_yn_z & -2n_yd \\ -2n_zn_x & -2n_zn_y & 1-2n_zn_z & -2n_zd \\ 0 & 0 & 0 & 1 \end{bmatrix}* \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} \]

Therefore, we get a matrix to transform point \(P\) to the mirror reflected point \(P'\).

In glm we can write a short function like XMMatrixRefect

glm::mat4 matrixReflect(glm::vec4 plane) {
    glm::vec3 normal{plane.x,plane.y,plane.z};
    plane /= glm::length(normal);
    return glm::transpose(glm::mat4{
        1-2*plane.x*plane.x,  -2*plane.x*plane.y,  -2*plane.x*plane.z, -2*plane.x*plane.w,
         -2*plane.y*plane.x, 1-2*plane.y*plane.y,  -2*plane.y*plane.z, -2*plane.y*plane.w,
         -2*plane.z*plane.x,  -2*plane.z*plane.y, 1-2*plane.z*plane.z, -2*plane.z*plane.w,
                          0,                   0,                   0,                  1
    });
}

auto model = glm::translate(glm::mat4(1.0),glm::vec3(1,0,0)); // model matrix to translate object to (1,0,0)
auto mirrored = matrixReflect(glm::vec4(1,0,0,0)) * model; // reflect the object with y-z plane, so the translation is (-1,0,0)

Winding Order Matters

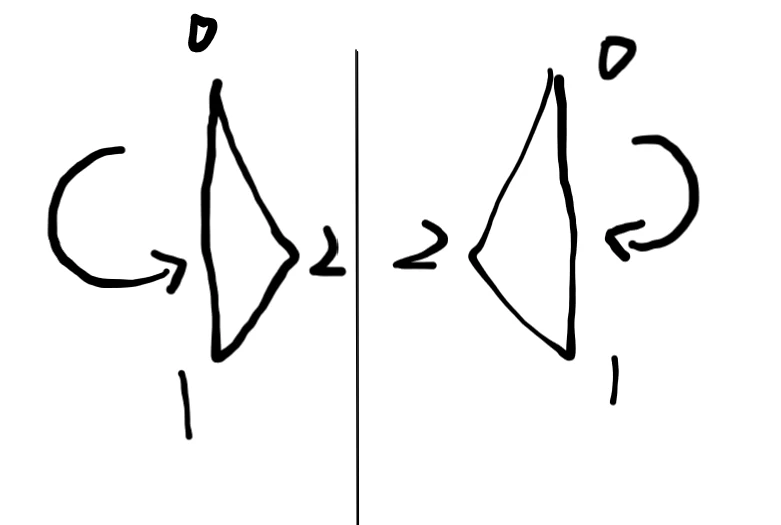
Rendering_Objects_Mirror_Reflected-2023-03-11-01-25-45

When an object is reflected by a plane, the winding order of its vertices will also change. This means the front face defined in the original models will now be recognized as back face, and will be culled by the pipeline if backface culling is enabled.

To avoid the issue, we can either disable the backface culling(discouraged) or change the winding order which defines front face.

glFrontFace(GL_CCW); 
DrawObject(...);

glFrontFace(GL_CW); 
DrawMirroredObject(...);

Rendering Plane Reflected Objects

Reflected matrix with a given plane

Winding Order Matters